Projects
PIC Microcontroller Assembly – Fibonacci
PIC 8-bit Microcontroller Assembly
I’m currently working on a project that I need a basic micro-controller for. I’m exploring potential options, and have some PIC chips on hand that I’d like to make use of so I’m considering using a PIC12F629, by Microchip.com. I’ve found the Microchip documentation and community to be quite helpful in getting started. It’s as simple as:
- Download & install MP Lab X IDE: http://www.microchip.com/mplab/mplab-x-ide
- Download & install an XC compiler: http://www.microchip.com/mplab/compilers
- Peruse the PIC12F69 documentation: http://ww1.microchip.com/downloads/en/devicedoc/41190c.pdf
- Read Page 9, 10 (Memory layout)
- Read Page 21, 22 (I/O Pin config)
- Read Page 71 (Instruction Set Summary)
- Refer to Page 72 (Instruction Table)
I’m interested in understanding the lowest level operation of the chip, so I’ve started with writing assembly instead of C. Here is a short and simple implementation of a Fibonacci sequence generator. Since this is an 8-bit chip, the maximum number I’m able to represent is 255, but for convenience of detecting the end of the generator, I end on the 16th step, which also demonstrates the 8-bit overflow.
; PIC 12F629 Register Addresses
#define INDF 0x00
#define STATUS 0x03
#define RP0 0x05 ; STATUS<RP0> bit selects the bank
#define FSR 0x04
#define GPIO 0x05 ; bank 0
#define TRISIO 0x05 ; bank 1
; Global Variables
#define TMP1 0x31
#define TMP2 0x32
#define FIB 0x20 ; fibonacci seq array
RES_VECT CODE 0x0000 ; processor reset vector
GOTO START ; go to beginning of program
; TODO ADD INTERRUPTS HERE IF USED
MAIN_PROG CODE ; let linker place main program
START
bcf STATUS, RP0 ; select Bank 0
; Build the fibonacci sequence in a memory block
movlw 0x20 ; start at 0x20
movwf FSR ; set the indirect addressing address
; Initialize sequence with 0,1
movlw 0x00 ; F_0
movwf TMP1 ; store it in working var
movwf INDF ; store it in memory block
incf FSR ; increment the File Select Register
movlw 0x01 ; F_1
movwf TMP2 ; store it in working var
movwf INDF ; store it in memory block
incf FSR; ; increment the File Select Register
; Continue the sequence from F_2 on
NEXT
; Add the two last numbers
movf TMP1,0 ; W = TMP1
addwf TMP2,0 ; W = W + TMP2
movwf INDF ; store W in data block at FSR
; update TMP1 and TMP2.. .tmp1=tmp2, tmp2=W
movf TMP2,0 ; W = TMP2
movwf TMP1 ; TMP1 = W
movf INDF,0 ; W = Value at FSR
movwf TMP2 ; TMP2 = W
incf FSR ; increment the File Select Register
btfss FSR, 4 ; skip goto when bit 4 of FSR is 1, eg FSR = 0bx1xxxx
goto NEXT
END
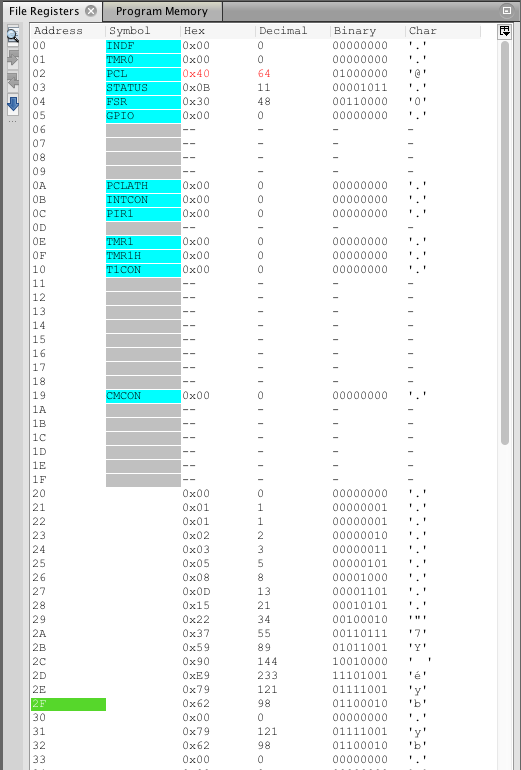
Here is a screenshot of the memory management tool in the MP Lab IDE’s simiulator:
Surely there are easier, more efficient, and/or more compact ways of writing this generator, but this is my naïve first attempt.
Robot Arm, Chess Computer Vision
The game of chess is one of the world’s most popular two-player board games. I often times find myself wanting to play even when no one is around to play. One solution to this problem is to play chess on a computer or mobile device against. However, many people would agree with me in thinking that playing a virtual game of chess is a completely different experience than playing a physical game of chess. For this reason, I intend to use this project as an opportunity to build a 6 degree of freedom robotic arm that will take the place of an opponent in a physical game of Chess. The state of the game will be determined by applying chess computer vision algorithms to images from a camera that will be mounted above the game board facing down.
The Setup
Chessboard
The chessboard used for this project is a standard wood chess board with 64 tiles, and 32 pieces.
The Robot Arm
I designed a 3R spatial manipulator in Autodesk Inventor 2013 and constructed the arm out of medium density fiber board. The joints are controlled by 7 servos connected to an Arduino microcontroller. I wrote a simple program for the Arduino that processes incoming serial commands that tell it joint positions in degrees.
Arm Design in Inventor
Camera Calibration
I calibrated by personal webcam for this project. The MATLAB Camera Calibration Toolbox was used to determine the intrinsic calibration parameters of my camera. I was surprised to find that my camera has very little radial distortion.
Distortion Example
The web cam introduces very little radial distortion, as can be seen by the images below
|
Distorted Image from Webcam |
After Undistortion |
 |
 |
Chess Computer Vision
My low target for this project is to identify the chessboard. I have managed to detect a calibration chessboard, and a real chess board. I did a little math to find the centers of the tiles which will be my starting point for determining if a piece is occupying the tile. For detecting the board I made use of libcbdetect.
Examples of Detected Chessboards
In these examples, the chess board has been identified and the centers of the tiles have been marked.
|
Black and White Calibration Chess Board |
Real Chess Board |
 |
 |
Potential Problem – Height of Chess Pieces and Perspective
One problem I ran into is that the height of some the Chess pieces causes the colored markers to appear outside of the tiles that the piece is in. This is due to the camera’s perspective on the scene. I reduced the extent of this problem by increasing the camera’s distance from the board.
Finding the Pieces
In order to identify the pieces from the top-down perspective provided by the camera, I attached colored pieces of paper to the top of each chess piece. In chess, each of the two players begins with 16 pieces, spanning 6 different classes. I assigned each of the 6 classes a unique color and attached hole-punched pieces of paper to the tops of each piece. The color of the piece of paper is used to determine the class of piece, while the color of the piece is used to determine if the piece belongs to player 1 or player 2.
The pieces are mapped to colors as follows:
| Chess Piece | Color |
| Pawn | Red |
| Rook | Green |
| Knight | Blue |
| Bishop | Pink |
| Queen | White |
| King | Orange |
LAB Color Space
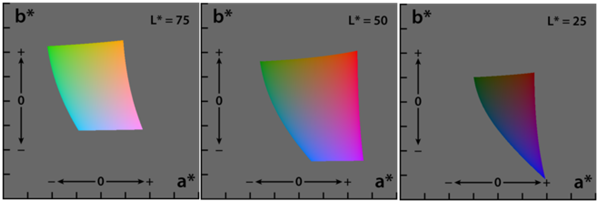
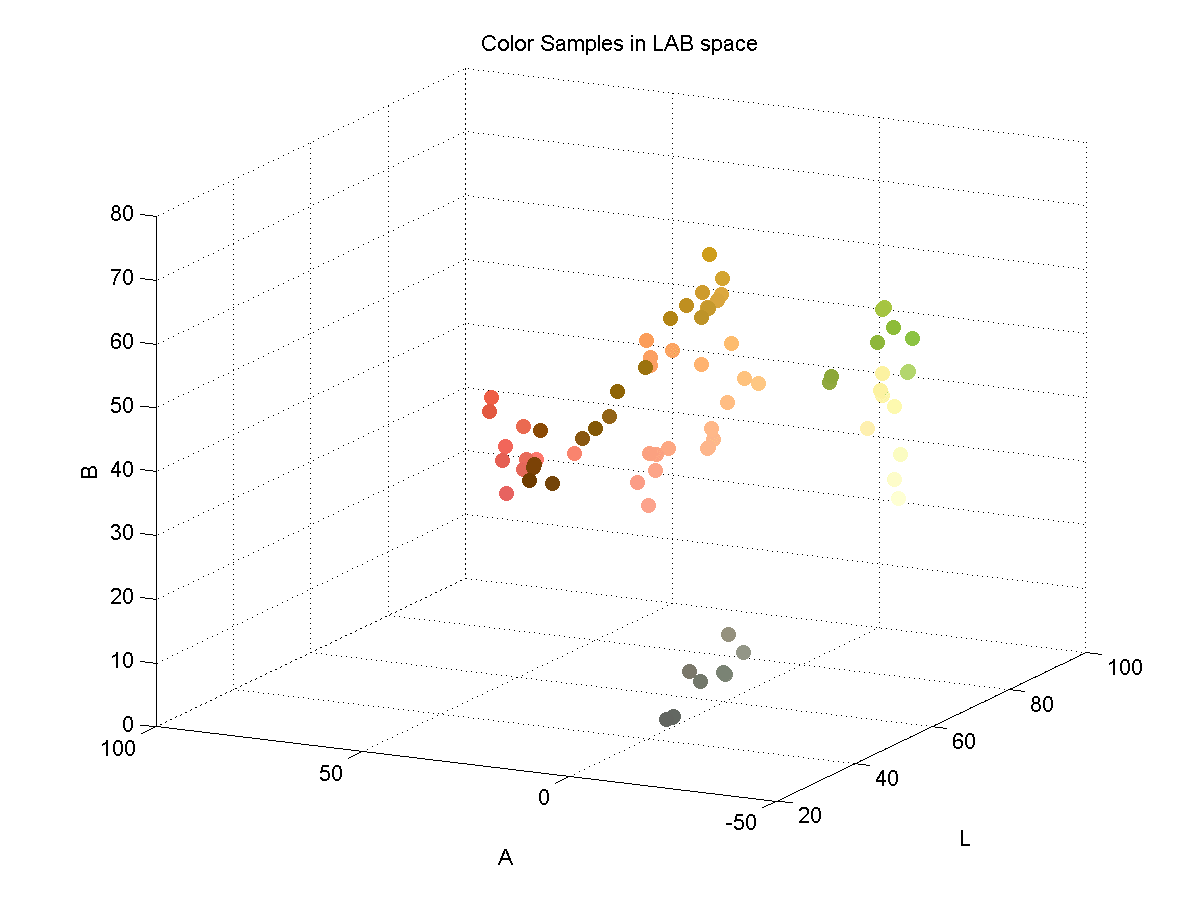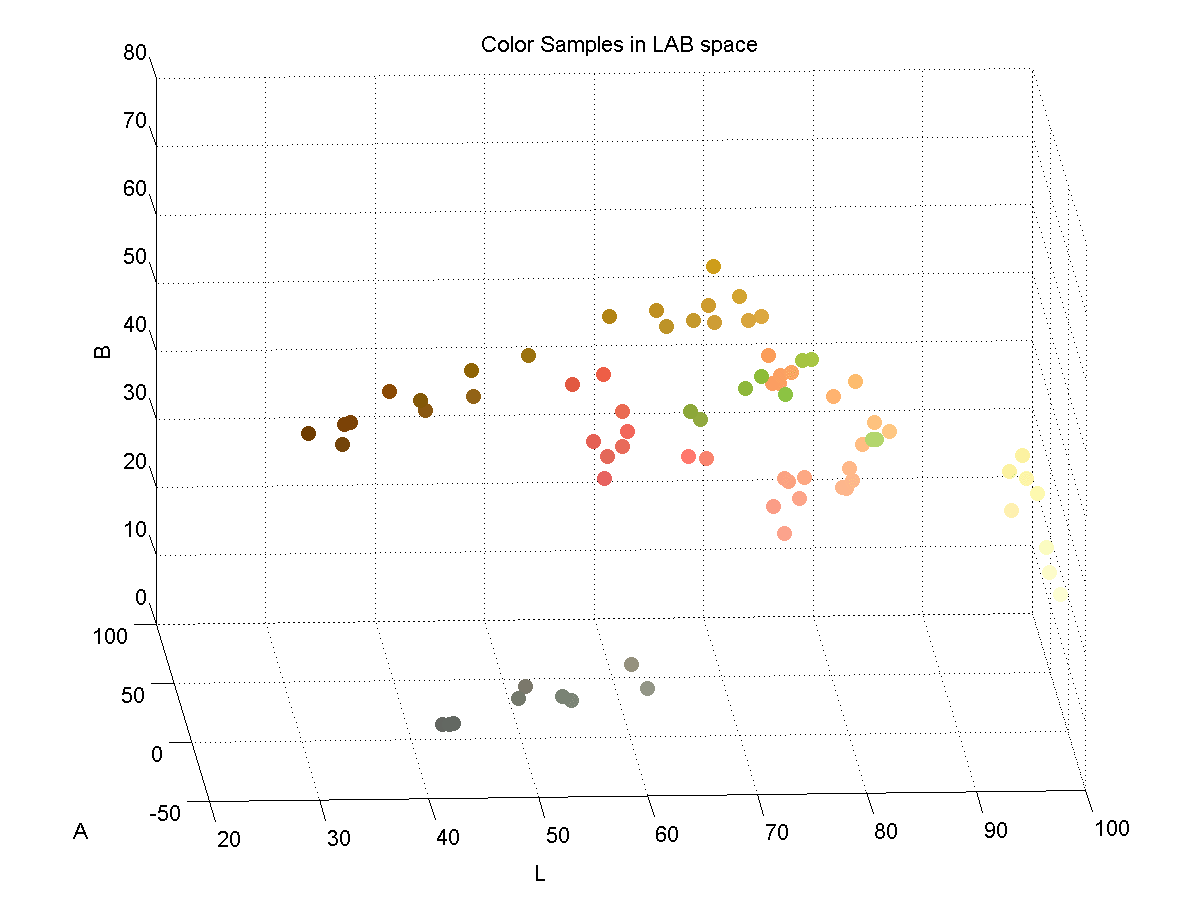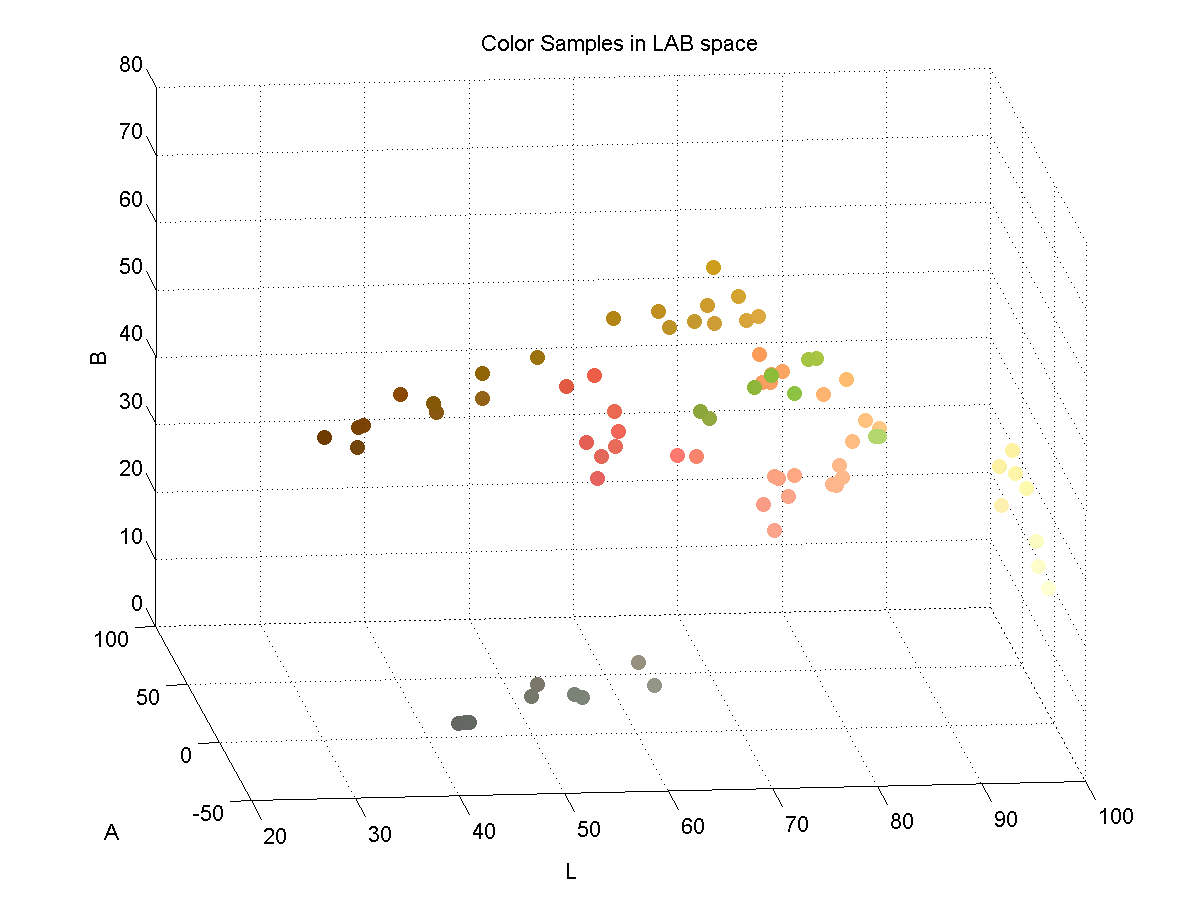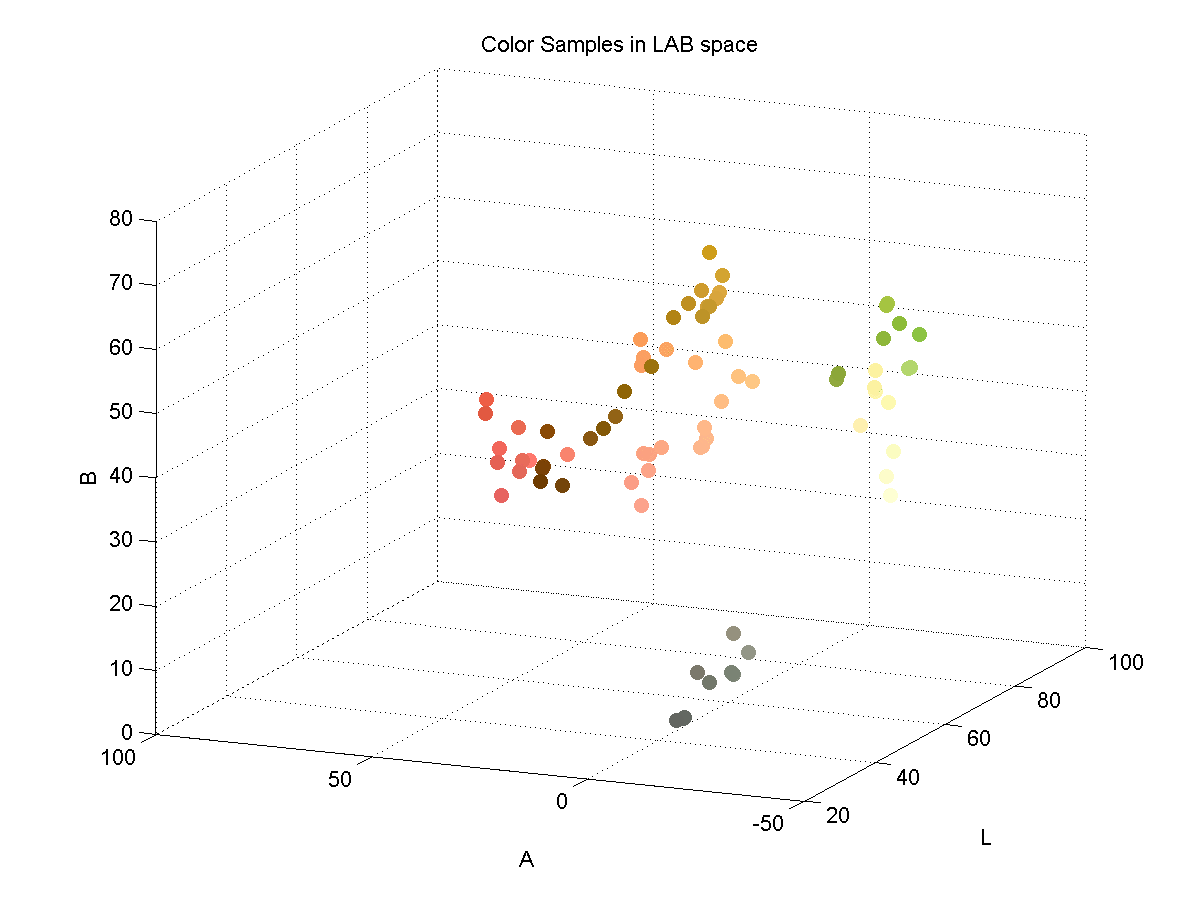
In order to effectively discriminate color, I had to find a color space that lent itself to this. I found that the LAB color space is common for color discrimination because it is more perceptually linear than other color spaces. To test its discriminative qualities for the purposes of this project, I took a few color samples of the potential colors for chess pieces and plotted them in LAB space. Here are three slices of the LAB space with varying L-values:
Here is a 3D plot of the color samples:
Color Identification
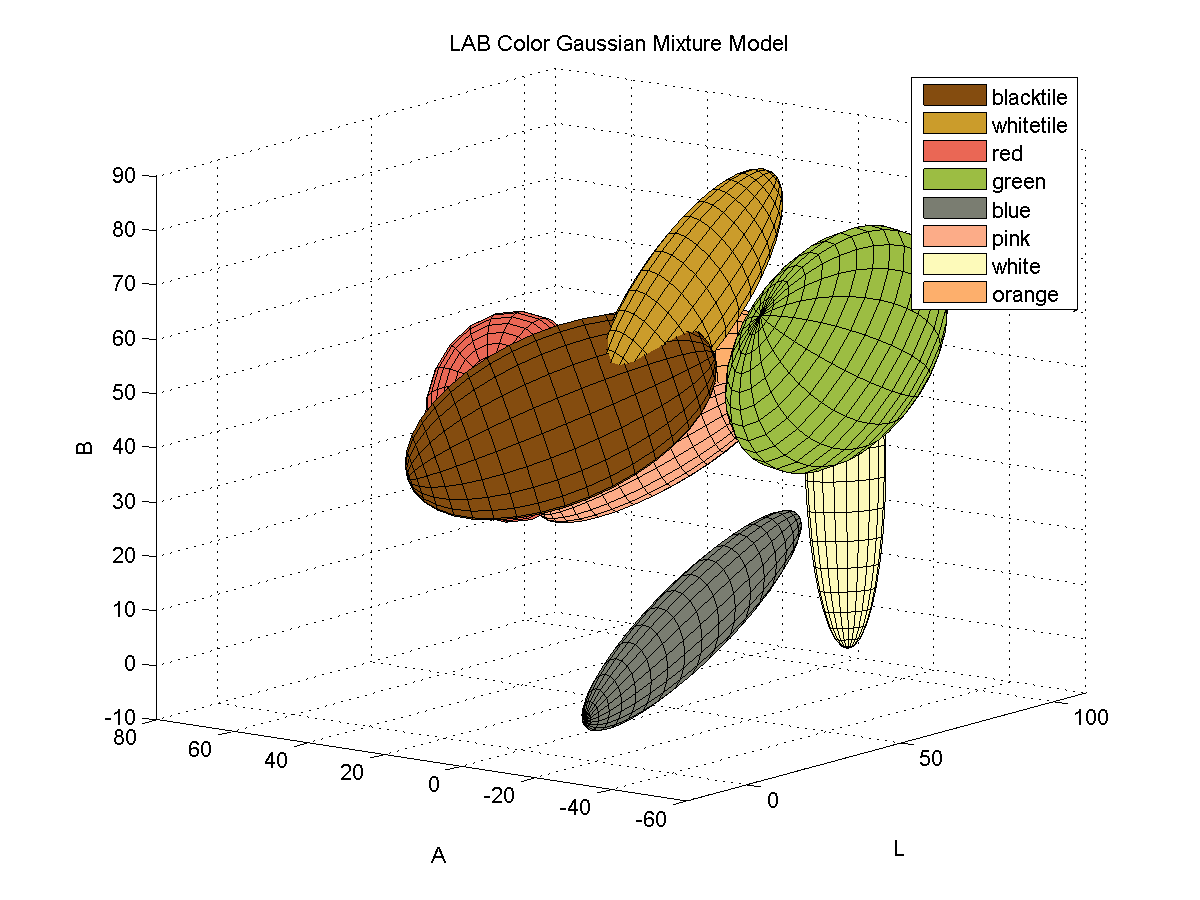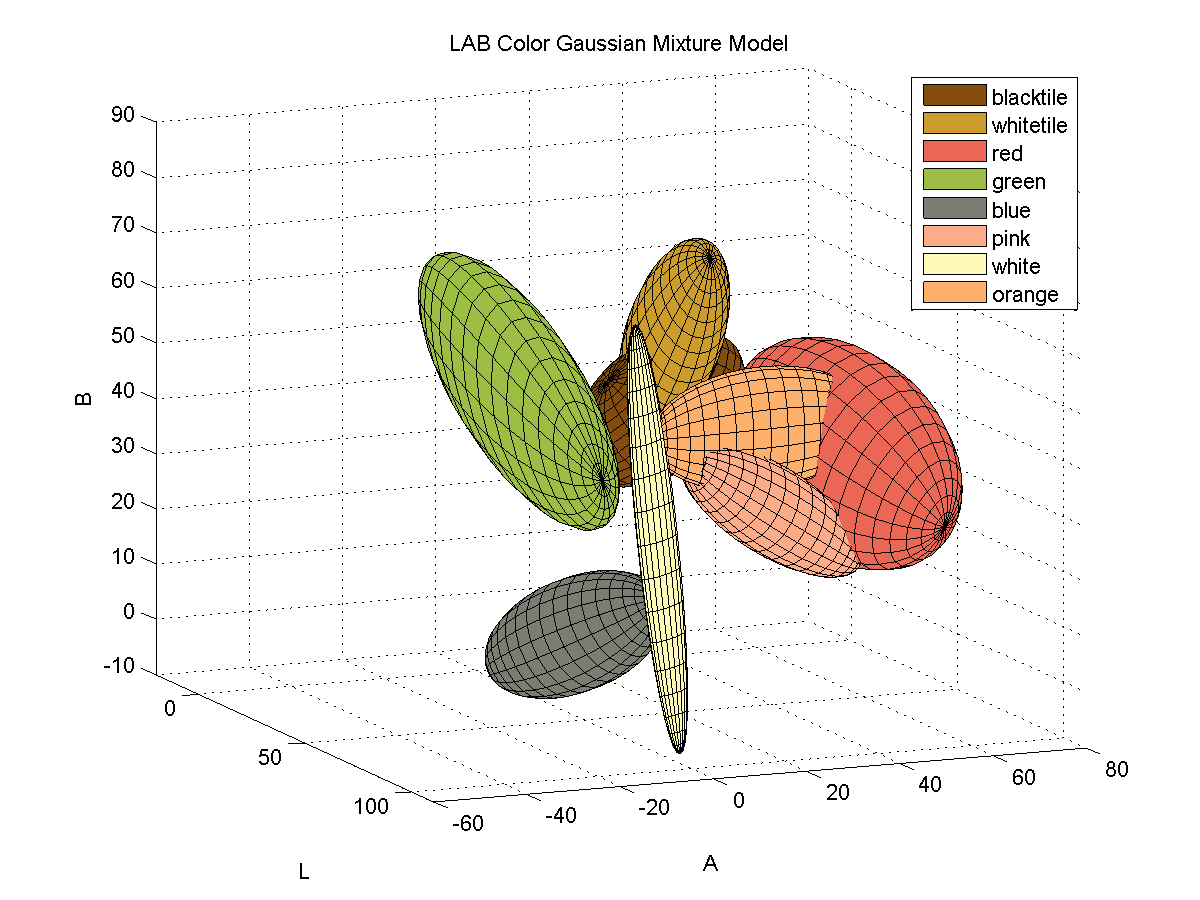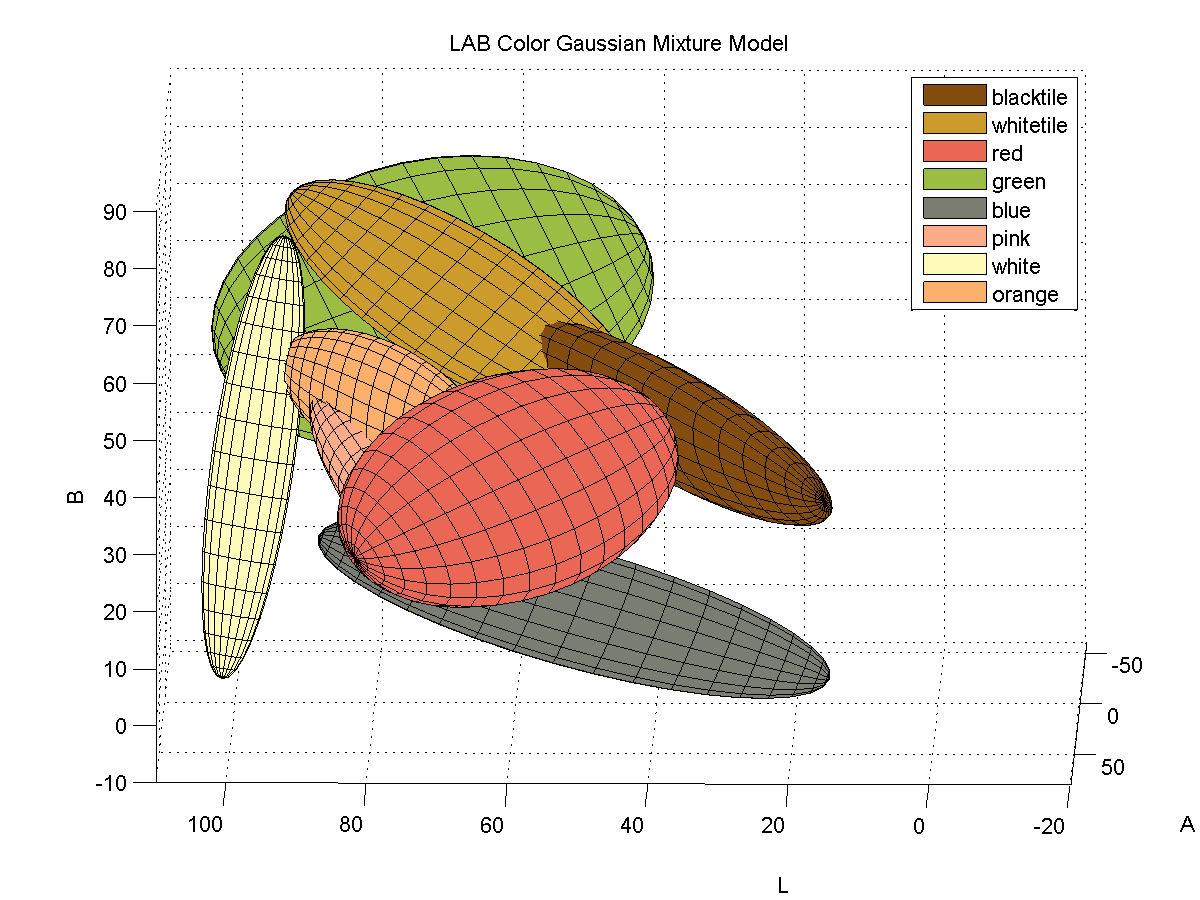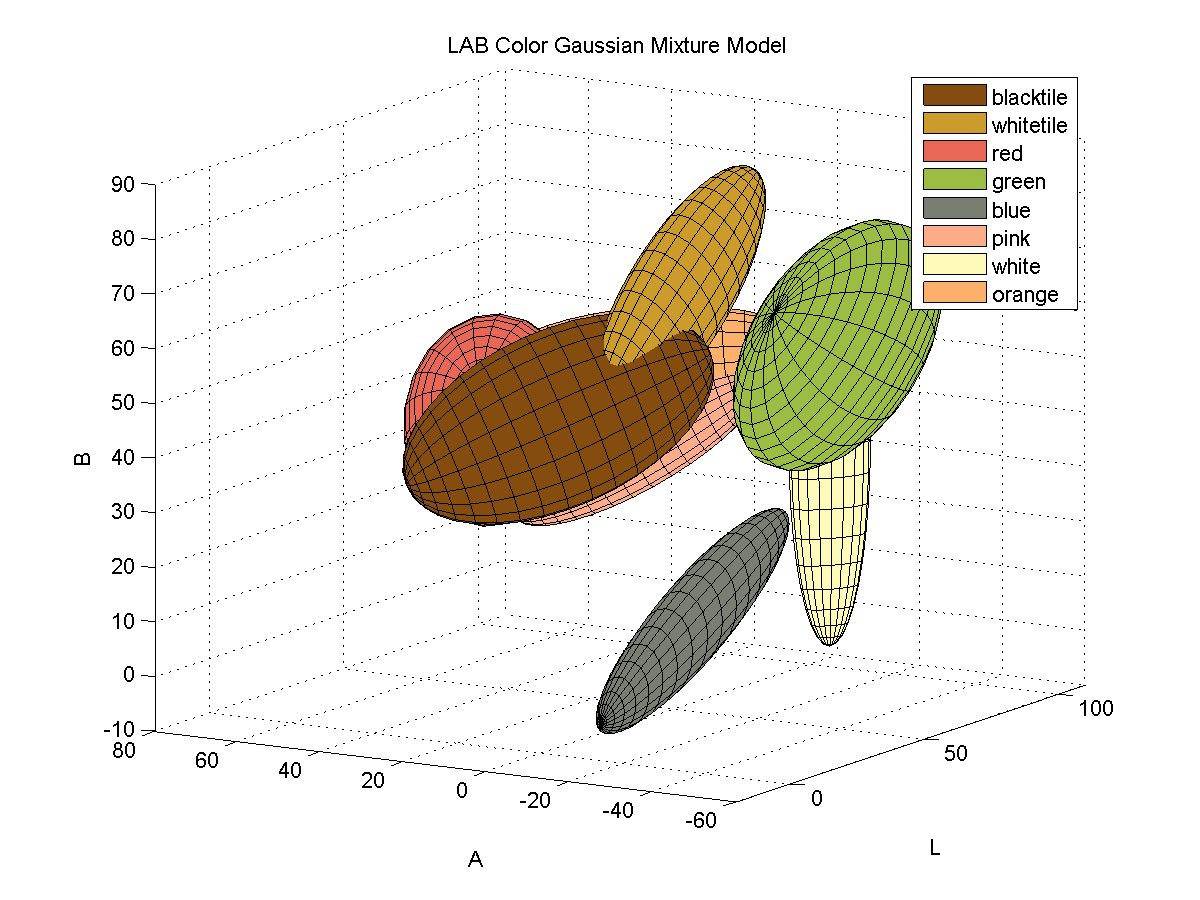
Color identification turned out to be quite a bit more difficult that I originally thought it would be. The variations in lighting caused a significant amount of variance in the detected colors. In order to capture the variance of the colors due to small variations in lighting I fitted color samples to Gaussian mixture models.
For each color, I collected samples of the color from images of the board with varying illumination and fitted the samples to a 3D Gaussian mixture model. Here is a depiction of the fitted Gaussians in LAB space. Each color is represented by a single Gaussian.
Segmenting Images by Color
In order to separate pieces from the board, I segmented the images based on pixel colors. To segment the image, I begin by converting an input image to the LAB color space. Then, for each pixel in the image, I compute the Mahalanobis distance from the pixel to each color’s Gaussian mixture model representation. I then find nearest Gaussian to the pixel and map the pixel to the color represented by said Gaussian.
Example Segmentation
| Input Image | Segmented Image |
 |
 |
From this point, I can easily isolate specific colors from the image.
Connected Component Blobs
Once the image is segmented, I calculate a binary mask that represents the locations of all of the chess pieces. I then perform morphological closing and opening to clean up the image and remove noisy color segmentation. Continuing with the output from the color segmentation above, here is the resulting binary mask of chess pieces:
This example contains perfect segmentation, but this isn’t always possible. For example, here is a noisy segmentation:
Usually noise results in blobs that are smaller than the actual chess pieces, so I remedied this problem by processing the blobs in order of decreasing size.
Identifying Pieces
To determine the class of piece for each blob detection I pull the index of the color of the isolated blob from the segmented image. Once the class of piece is detected, I must detect which players piece it is; black or white. Determining if the piece is black or white is accomplished by analyzing color samples along a line from the centroid of the blob to the center of the chess board. I only collect samples that are right outside the edge of the color blob, because this is the location where black or white pixels are.
For example, here is a detected white pawn. The blue line represents the offset from the center of the detected blob to the tile center. The green line represents the locations where color samples were collected for determining if the piece is white or black.
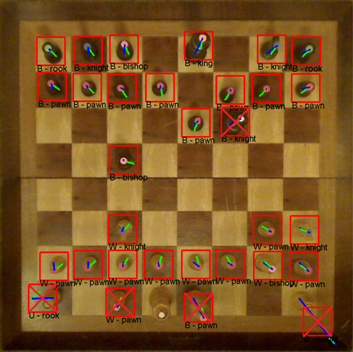
Here are examples of chess piece classification. From the images below, it is clear that variations in lighting cause problems for the classification process. I may be able to build a more robust model for representing the colors by using more color samples across a wider range of illuminations. It may be worthwhile to consider using Gaussian mixture models with more mixture components per color.
Problems
Here are some of the problems I ran into during this project.
- Variations in Lighting
- Possible Solutions:
- Use more diverse color samples for GMM’s
- Use multiple Gaussians per color
- Possible Solutions:
- Real-time
- Webcam auto adjustments (focus, lighting)
- Chess board & Pieces
- Glossy finish causes color misclassification